이쁜왕자 만쉐~~
1^x = 2 본문

인터넷을 돌아 다녀 보면 1^x = 2 라는 문제가 있고, 이것의 해를 어떻게 구하는지에 대한 설명이 나온다.
사실 고등학교 수학 수준에서는 어떤 x 에 대해서도 1^x = 1 이어야 하므로, 이 문제의 해는 존재하지 않는다.
문제는, 이 것이 대학교 수준으로 가서 '복소해석학'과 결합되면 신기하게도 해가 존재한다. 이는 log (-1) 이 고등학교 수준에서는 정의되지 않지만, 대학교에서는 정의할 수 있는 것과 비슷하다. https://www.valken.net/573 참고

여튼 이 식의 답을 얻기 위해서는 '오일러의 공식'에서 유래되는 e^(2n pi i) = 1 이 필요하다. 그냥 냅다 이 식을 집어 넣고 양변에 log 를 취해서 답을 구하면, 아래와 같은 해를 구할 수 있다.

사실 중간에 2n pi 때문에 식이 살짝 변형되기 때문에, 울프랑 알파 같은데 넣어 보면, 아래와 같은 답으로 튀어 나온다.

해를 구했으니 끝... 이 아니라 검산을 해봐야 한다.
다만, 검산을 해보기 전에 지수함수의 분수 지수를 이해해야 한다.
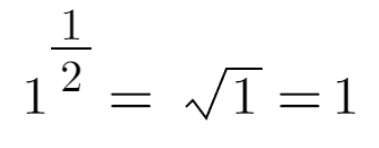
일단 1^(1/2) 을 계산할 수 있어야 한다. 1^(1/2) = √1 = 1 이라고 생각한다면, 아직 고등학교 수준이다. 이 경우에도 e^(2n pi i) = 1 를 냅다 넣고 계산하면, 아래와 같이 된다.
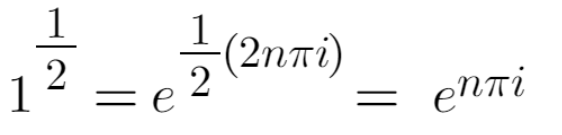

e^(n pi i) 에 정수 n { ... , -2, -1, 0, 1, 2, ... } 을 차례로 넣으면 { ... , 1, -1, 1, -1, 1, ... } 이 되어, 1 과 -1 이 반복해서 나온다. 다시 말해 1^(1/2) 은 다가함수이고, 그래서 이런 식을 성립하게 만드는 이유가 된다.

같은 방법으로 1^(1/4) 을 계산해 보면, { 1, i, -1, -i } 가 반복되는 다가함수로 나오며, 1^(1/100) 은 100개의 주기를 가지는 다가함수가 된다.
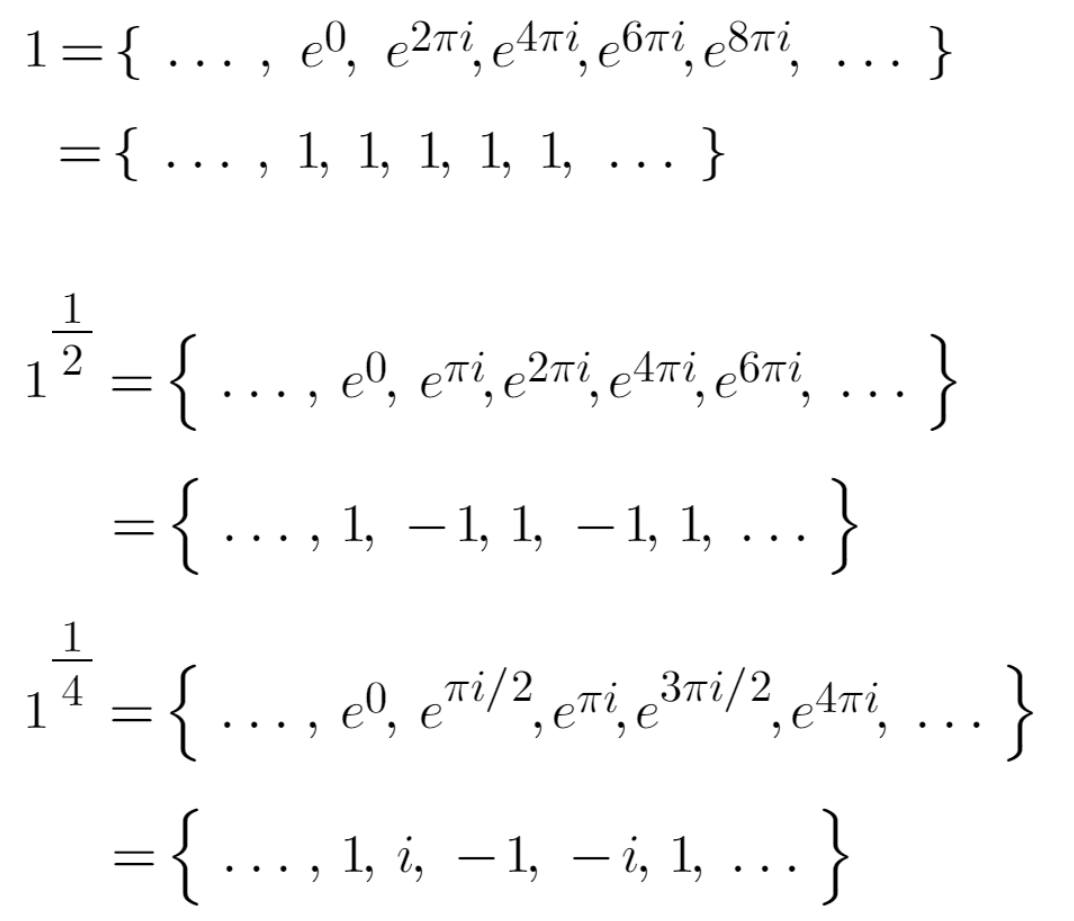
일단 분수(유리수) 지수에 대해서 생각해 보았지만, 유리수가 아닌 무리수이거나, 심지어 복소수 지수 인 경우에도 정의가 가능하고, 비슷한 결과를 얻을 수 있다.
그래서, 지수 함수는 그 자체로 복소수 범위에서 다가함수로 정의되고, 심지어 실수 1 도 무한한 1로 정의되는 다가함수로 쓰는 것이 가능하다.
복소수 지수 함수를 정의하려면 여러 엄밀한 조건이 필요하지만, 별아저씨님의 간략한 설명만 따오면 아래와 같다.
| 1. 먼저 exp(z) 를 exp(x)가 무한급수로 정의되는 것과 같이 정의하고 그 무한급수가 모든 복소수 z에 대하여 수렴함을 보임으로써 잘 정의됨을 안다. 2. logz를 expz의 역힘수로 정의한다 단 expz가 다대일 함수이므로 영역 설정에 주의한다. 3. expz 와 logz을 이용하여 실변수일 때의 등식 a^x=e^xloga 를 이용해서 a^z=exp(zloga)로 정의한다. 이러면 a^z는 다가함수가 된다. |
이해가 안되면, 정상이다. 이 내용들은 대학교 수학과에서 '복소해석학'을 수강해야 튀어 나오는 내용들이다.
다시 검산으로 돌아 가서, 가장 간단한 형태인 m = 0, n = 1 인 을 대입해서 계산해 볼 수 있는데, 아이러니하게도 다시 e^(2n pi i) = 1 이 쓰인다. 어떻게 보면, 계산의 역순이라 검산의 의미가 있는지 모르겠다.
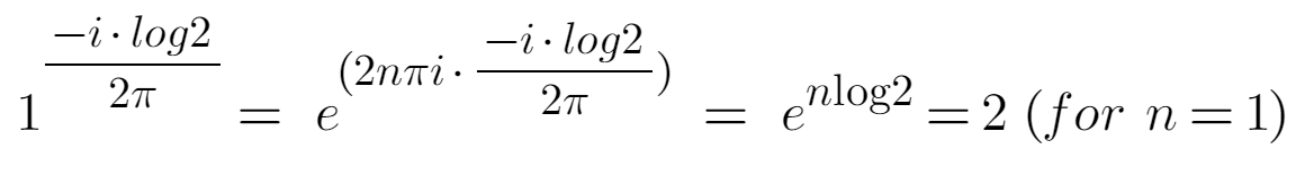
사실 여기서 다가함수가 다시 쓰이기 때문에, 수많은 값들이 튀어 나올 수 있고, 그 값중에 하나가 2 이다. 라고 해석해야 한다.
수학은 어렵다.




