목록퍼즐판 (62)
이쁜왕자 만쉐~~
 주사위로 사용되는 기하학적 도형
주사위로 사용되는 기하학적 도형
주사위 하면 떠올리는 가장 기본적인 형태는 정육면체 이다. 그러나, 주사위는 정육면체만 있는 것은 아니다. 다양한 면을 가진 주사위가 존재하며, 실제로도 널리 쓰인다. 주사위의 기본이 되는 모양은 5종류의 정다면체이다. 4, 6, 8, 12, 20 면을 가진 5가지 종류의 주사위가 기본으로 존재한다. 10면체 주사위(d10) 정육면체를 포함하여 5가지 정다면체는 모두 주사위로 쓰인다. 그런데, 위의 주사위 모음을 보면, 정다면체가 아닌 주사위가 있는데, 이는 10면체 주사위 이다. 100까지 사용할 수 있도록 0 ~ 9 가 적인 주사위와 0, 10, 20, ... , 90 가 적힌 2개의 10면체 주사위가 존재한다. 이 10면체는 연(kite) 라고 부르는 사각형 10개로 만들어진 pentagonal t..
5 를 제곱하면 25 인데, 5로 끝난다. 25를 제곱하면 625 인데 25로 끝난다. 625를 제곱하면 390625 인데 625 로 끝난다. ... 8212890625를 제곱해도, 8212890625 로 끝난다. 이렇게 어떤 수 n 을 제곱했는데, 제곱수의 마지막이 n 으로 끝나는 수를 automorphic number 라고 부른다고 한다. 1자리수 기준으로 이것이 성립하는 수는 0, 1, 5, 6 이렇게 4가지 이다. 그리고, 이것들은 자리수를 계속 늘여도 이 조건이 성립한다. 일단 0 과 1 을 보면 000...000 은 그냥 0 이고 제곱해도 0 = (000...000) 이다. 000...001 은 그냥 1 이고 제곱해도 1 = (000...001) 이다. 수 앞에 0 을 붙이는 것이 허용된다고 ..
 [퍼즐] 정삼각형은 몇개가 필요한가?
[퍼즐] 정삼각형은 몇개가 필요한가?
동일한 크기의 정삼각형 타일이 아주 많이 있다. 이 정삼각형 타일들을 맞붙혀서 여러 볼록 다각형을 만들고자 한다. 정삼각형 타일 1개로 만들수 있는 것은 당연히 삼각형뿐이다. 만약, 타일이 2개라면 두개를 맞 붙혀서 사각형을 만들 수있다. 3개인 경우도 역시 사다리꼴 형태의 사각형을 만들 수 있다. 만약, 타일이 4개라면, 커다란 삼각형을 만들 수도 있고, 사각형을 만들 수도 있다. 즉 2종류의 다각형을 만들 수 있다. 만약, 타일이 6개라면 육각형을 만들 수 있고, 사각형을 만들수 있다. 만약, 타일이 7개라면 오각형을 만들 수 있고, 사각형도 가능하다. 위의 경우를 보면 알 수 있듯이 타일의 수에 따라 두가지 이상의 다각형을 만들 수 있는 경우가 있다. 그렇다면, 삼각형, 사각형, 오각형, 육각형을 ..
 [퍼즐] 고전 퍼즐 - 곰의 색깔은?
[퍼즐] 고전 퍼즐 - 곰의 색깔은?
어떤 사냥꾼이 곰을 쫓아서 남쪽으로 1km 갔다가, 동쪽으로 1km를 갔다가, 북쪽으로 1km를 갔더니 자신의 처음 위치로 돌아 왔다. 곰의 색깔은? 이러한 퍼즐이 있는데, 꽤나 오래된 고전 퍼즐 문제이다. 문제 출제자가 의도한 답의 위치는 '북극점'이고, 북극에는 하얀 북극곰이 살고 있으니 곰의 색은 '흰색'이다. 이 문제는 살짝 변형되어 특목고 모의고사 문제로 출제된적도 있다고 한다. 그런데, 이 문제는 그렇게 단순하지는 않다. 수학/물리학적인 관점
까막옹이 문제를 냈으니,, 풀어주는게 인지상정. 간만에 퀴즈 타임.감옥에 갇힌 50명의 수학자들이 석방을 놓고 간수와 게임을 합니다. 게임의 규칙은 다음과 같습니다.1) 수학자들은 한 번에 한 명씩 테이블이 있는 방에 들어옵니다.2) 테이블에는 A, K, Q 각 한장씩 세 장의 카드가 있고, 카드를 놓을 수 있는 자리가 3곳(1, 2, 3번) 있습니다.3) 1~3번 자리에는 각각 카드가 없을 수도 있고, 카드가 1장 있거나, 2장 있거나, 3장의 카드가 전부 놓여 있을 수도 있습니다. 초기 상태는 간수 마음대로입니다.4) 모든 카드들은 전부 앞면이 보이도록 놓여 있지만, 여러 장이 한 자리에 겹쳐 있을 경우 맨 위의 카드만 확인할 수 있으며, ***몇 장의 카드가 겹쳐 있는지는 알 수 없습니다.*** A..
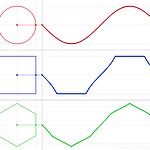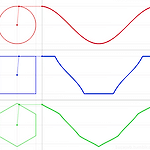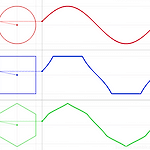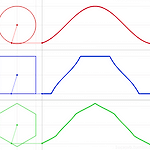 각진 SIN 그래프 ...
각진 SIN 그래프 ...
오유 게시판에 이런 그래프를 어떻게 그리는 지에 대한 글이 올라왔다. SIN 함수를 어떻게 뜯어 고치느냐는 문제이다. 첫번째 그래프는 그냥 일반적인 SIN 그래프니깐 패스.. 두번째 그래프의 경우는, 기본적으로 탄젠트 그래프이다. 그걸 max 1, min -1 로 제한하면 원하는 그래프가 나온다. 다만, 방향성이 문제가 되어 tan(x) 를 그냥 쓰는 대신에 sin(x)/|cos(x)| 로 살짝 변경하면 원하는 그래프가 나온다. 그래서 처음에 이런식으로 그려 보았다. http://www.wolframalpha.com/input/?i=plot+y%3Dmin%28max%28sin%28x%29%2F%7Ccos%28x%29%7C%2C-1%29%2C1%29+%2C+0%3Cx%3C2*pi%2C+-2%3Cy%3C2 ..
 1-1+1-1+ ... = ?
1-1+1-1+ ... = ?
1 과 -1 이 무한히 번갈아 나오는 수열의 합은 얼마인가? 즉 1-1+1-1 ... 은 얼마인가? 1 과 -1 을 하나씩 묶어서 (1-1) + (1-1) + .., 이라고 쓴다면 그 값은 0 이 될 것이다. 처음 1은 넘기고, -1과 1을 하나씩 묶어서 1+(-1+1)+(-1+1)+... 라고 하면 그 값은 1 이 될 것이다. 고전적인 수학에서는 이 값은 하나로 결정되지 않으므로, 진동한다고 표현한다. 아니면, 그냥 특정 값을 가지지 않는다고 표현해도 무방하다. 하지만, 수학자들은 뜬금 없는 황당한 가정을 많이 하는데, 이 경우라면, 이 수열의 합을 하나의 수로 표현할 수 없을까? 라는 가정이다. 좀더 일반적인 이야기를 하기 위해서, 초기항이 1 이고, 등비가 r 인 수열 A_r(n) 을 생각하고, S..
시작이 1 공비가 r 인 무한 등비급수 가 있다고 하자. 이는 1 + r + r^2 + r^3 + ... 인데, -1
문제1) 임의의 서로 다른 두 무리수 a < b 가 존재하여, a < c < b를 만족하는 유리수 c가 반드시 존재하는가? 너무나 당연해 보이지만, 막상 증명해 보려면 으음? 하고 고개가 갸우뚱했던 문제이죠. 두 수 a, b 를 각각 십진 소수 전개를 하면, 두 수는 서로 다르므로, 자리값이 다른 자리수가 반드시 나옵니다. 예를 들어 a = 0.12345678812.... b = 0.12345678912.... 라고 할때, c 를 다음과 같이 정의 합니다. c : "b 에서 a 와 서로 다른 자리값이 나온 곳에서 자른 수" 위의 예제에서는 c = 0.123456789 c 는 유한소수 이므로 당연히 유리수입니다. 또한 당연하게 a < c < b 입니다. 문제 2) 임의의 서로 다른 두 유리수 a' < b'..
a^c = b 를 만족할때 log_a (b) = c 또는 log(a,b) = c 라고 표현된다. 특히 a = e 일때를 자연로그 (보통 ln 으로 표기), a = 10 일때를 상용로그 (보통 lg 로 표기), a = 2 일때를 이진로그 (보통 lb 로 표기) 하여 구분한다고 하는데, ln 말고는 잘 안쓰인다. 그리고, 고등학교 교과과정에서는 로그에 대해서 a 는 1 이 아닌 0 보다 큰 실수, b 는 0 보다 큰 실수로 한정한다. 이렇게 범위를 한정하는 이유는, 저 조건을 만족해야 실수 범위 내에서 정의되기 때문이다. 하지만, 수학의 세계는 넓고도 오묘해서 log 를 음수뿐만 아니라 복소수 범위로 확장해서 적용하는 것이 가능하다.(주1: 이 글에서는 편의상 밑이 표기 안된 log 는 자연로그 ln..
